出于对汽车的兴趣以及专业的惯性,自己很久之前就开始想象未来汽车以及驾驶的发展方向。待到动手开干时,彼时的特斯拉股价还只有区区$300。那段时间对课题方向很迷茫,甚至想把自己的课题也改成自动驾驶方向。但是无奈,仅凭现有的导师资源,难以应付工程实现难题,以及理论基础的空缺,作为主要研究方向的话,恐怕难以跻身学界的第一梯队。
于是作为纯兴趣,没有外部支持,要开始的话那一切任何软硬件方案都需要从零构建组合。某一天在树莓派论坛闲逛时,发现了RoadApplePi这个开源项目。这个项目利用了obd2接口,实现了车载黑匣子的功能,而且整套硬件的成本可接受,读取车辆信息只需要能解码obd口的芯片和树莓派。继续顺藤摸瓜发现,基于elm327芯片的方案,虽然成本低廉,但是不能获取更全面的信息,而且非常难用。想要真正地黑到所有车载电脑信息,需要获取更底层的CAN数据。记得有一篇丰田和英伟达合作的自动驾驶文章,就是直接用can作为通讯接口。自己尝试了以下两种方案
另外有一些英文社区和b站的项目使用了pican 2这个板子,配合树莓派使用,价格低于以上两种,但是在车上使用的树莓派安上了显示器,不再适配这种方案,遂放弃。两种方案最大的区别是,CANalyze是有线连接而Panda是wifi连接。软件端均有Python包支持,非常方便。
Panda不仅仅解决了获取信息,直接让我了解到 comma.ai 这个公司是做开源自动驾驶解决方案的。算法实现林林总总,但是直接把产品级别代码开源也是大开眼界。好处是显然的,对于学习自动驾驶的技术栈,有了一个非常好的参照物。
想得到汽车的状态数据,需要经过一些繁琐的实验,确定每一种数据在can总线中物理地址,之后用简单的脚本就可以像飞机黑匣子一样记录汽车的操控数据(主要是油门,刹车,方向盘角度和力矩)和运行状态了!从哲学角度,有了这些数据,就可以回答小车车对自己提出的“我是谁”的问题了。
对于后两个哲学问题,“从哪里来”和“到哪里去”,显而易见,首先需要对车进行定位。市面上很多款行车记录仪配备gps功能,但是不是所有的产品都方便获取原始的gps数据,比如rexing。行车记录仪只是一时之计,想要统一到一个系统可以用usb gps模块,通常低于20USD。图像和定位信息暂时从行车记录仪解决了,虽然精度不高,时间上采样频率是1Hz, 空间上单条轨迹相对的位置精度还好,但是每次连接卫星,都会有不同的偏移,估计有1m-10m的误差。(没上过测量学,不知有什么解决方案)
实现以上步骤,花了有一年多,终于是有一套简陋但是信息相对完整的驾驶数据集。理论上可以开始构建自动驾驶的算法了,但是“到哪里去”又成了一个意外的难题,博客的后半部分也是探究一下解决方案。
问题源于自己车上的方向盘角度传感器在ecu启动时默认设置为归中位也就是0,无论此时方向盘是否真的回正。这就导致每次旅程记录的方向盘角度都有一个未知的偏移角度,不能消除这个偏移,也就无法正确识别小车当前前进方向,更无从谈起自动驾驶。图像识别也许可以帮忙,但是需要额外的大量算力,倘若通过算法让车机自动校正呢?
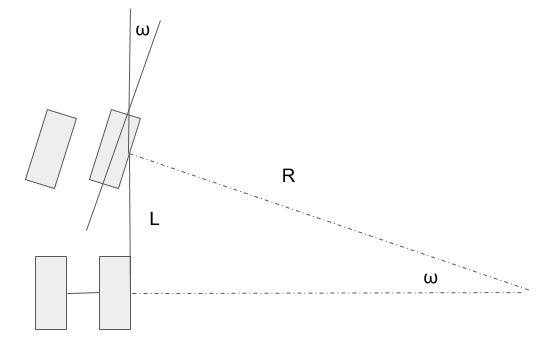
使用一个简化的模型,车辆轴距为L,此时车轮偏转 $\omega$ 角度,转弯半径约为
$$R = \frac{L}{\sin{\omega}}$$
当车辆速度为$v$,经过$\Delta t$时间后,航向角偏转$\Delta \psi$ 为
$$\Delta \psi = \frac{v(t) \cdot \Delta t}{R}
$$
$\omega$与方向盘偏移角度的关系因车而不同,且可能随速度变化,此处假设低速情况下成正相关,系数为$\alpha$
$$\omega = \alpha (X(t) - \Delta)
$$
其中$X(t)$为$t$时刻的方向盘偏移角,$\Delta$为我们要求的初始偏移角。合并后得到
$$
\Delta \psi = \frac{v(t) \cdot \Delta t \cdot \sin(\alpha(X(t) - \Delta))}{L}
$$
从公式上看当$\Delta \psi = 0$,有$\Delta = X(t)$,那么如果从数据中找到直行的数据点,那么此时方向盘的角度读数即为偏移角度。实际情况中,由于方向盘采样频率高(>>1Hz)而坐标的采样时间和空间频率低,严格的$\Delta \psi = 0$极少出现,而在$0$附近$X(t)$呈现一种分布,简单方法是求分布的均值。比如下图数据集,可以估算出偏移角$\Delta$约为$-7.5$度。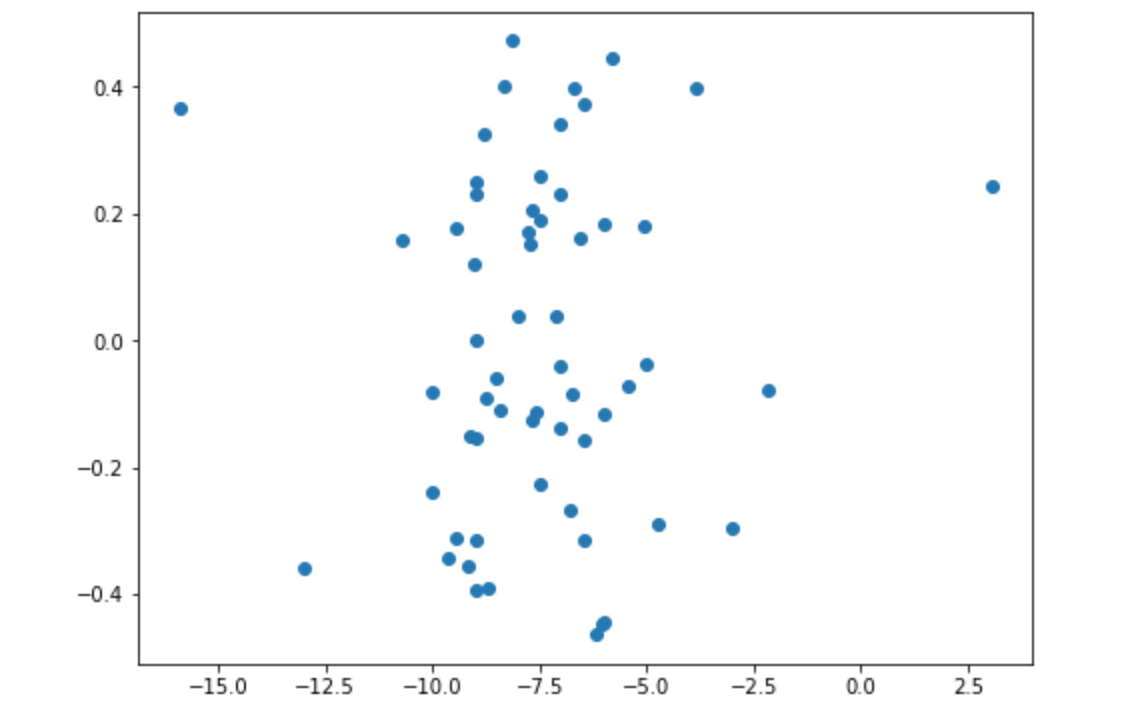
这种方法无法获得一种统一而且收敛的结果,0值的临域和采样的时间范围都是变量,且波动不小。
另一方面可以求解积分形式
$$
\Delta \psi = \int^{t1}_{t0}\frac{v(t) \cdot \sin(\alpha(X(t) - \Delta))}{L} dt
$$
当车轮偏转角度不大时可近似为
$$
\Delta \psi = \frac{\alpha}{L} \int^{t1}_{t0}v(t) \cdot (X(t) - \Delta)) dt
$$
此式引入了未知常量$C = \frac{\alpha}{L}$,可以控制的参数是起始和结束时间$t0$和$t1$,其求解超出我的当前的知识范围,能想到的解法是,搜索一个合适的$C$,求出满足积分方程$\Delta$的值,在不同$t0$和$t1$下。合适的$C$应该使得不同$t0$,$t1$组合下,$\Delta$的解为常值,得到的常值应为估计值。才疏学浅,希望有高人指点,给出一个干脆利落的解法!
未来驾驶,不限于自动驾驶,一定有各种传感器组成基础设施。采集得来的驾驶数据就是ai的燃料。因为隐私的问题,一定会像其他ai数据集一样成为双刃剑。除非有一天道路上的车全部由一套系统统一控制,在此之前,人和无人车的对抗、ai和ai之间的对抗会一直存在。还有一点,相信有人和我一样是能享受驾驶的乐趣,虽然前路还不太明确,但是我想象中的未来驾驶的场景会保留住有人驾驶这一核心。特斯拉股价1500了,如果之前的硬件投资买一股,现在够多配一块2080ti 或者Livox LiDAR了。